top of page

Portafolio de Evidencias Precálculo
Jordain Rodríguez Diez

SECCIONES CÓNICAS
Circunferencia:
Forma que debe tener:


Parábola:
Ejemplo:
y^2-4x-4y+16=0
Ejemplo:
4x^2+4y^2+3x-2y-51=0
(x-h)^2+(y-k)^2=r^2
C (h,k) radio r
Forma que debe tener:
(y-k^2) = 4p(x-h)
V(h,k)


Elipse:
Hay dos tipos de elpise: La horizontal y la vertical
Forma que debe tener la horizontal:

Forma que debe tener la vertical:

Los dos tienen el punto medio en C (h,k)
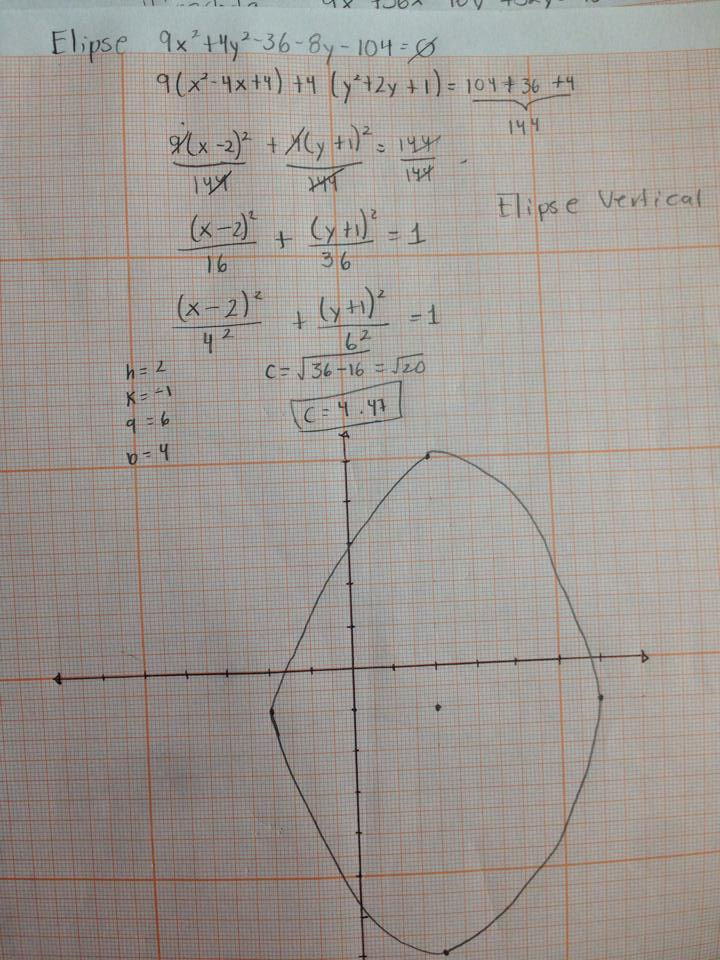
Ejercicios

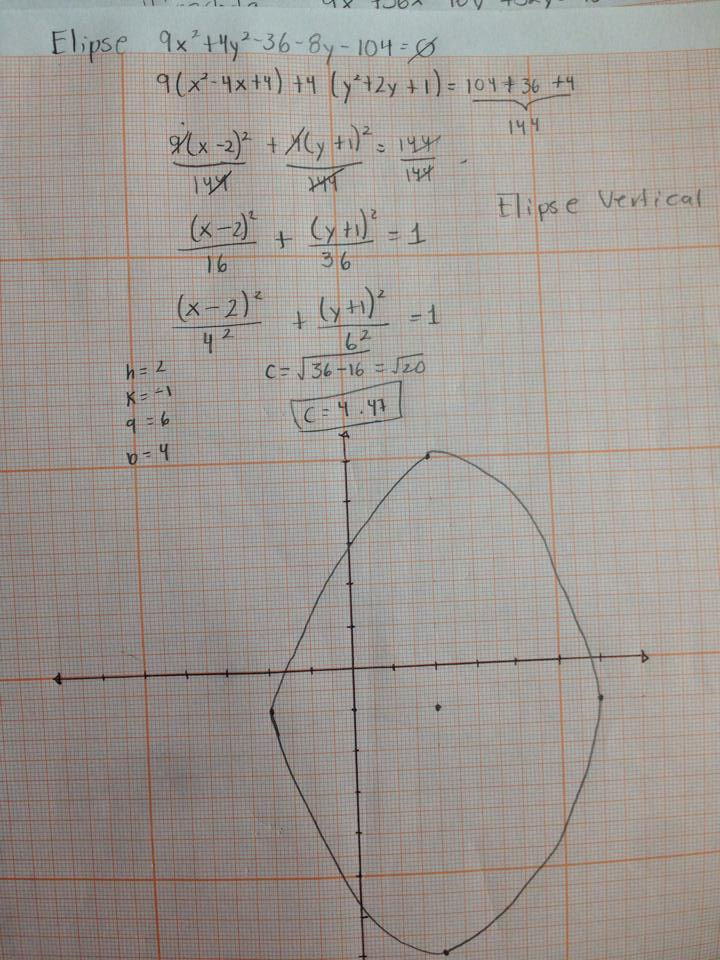
Ejercicios
1/2
-
La distancia del centro al vértice es a
-
La distancia del centro al foco es c
Hipérbola:

c<a a diferencia de la elipse a<c
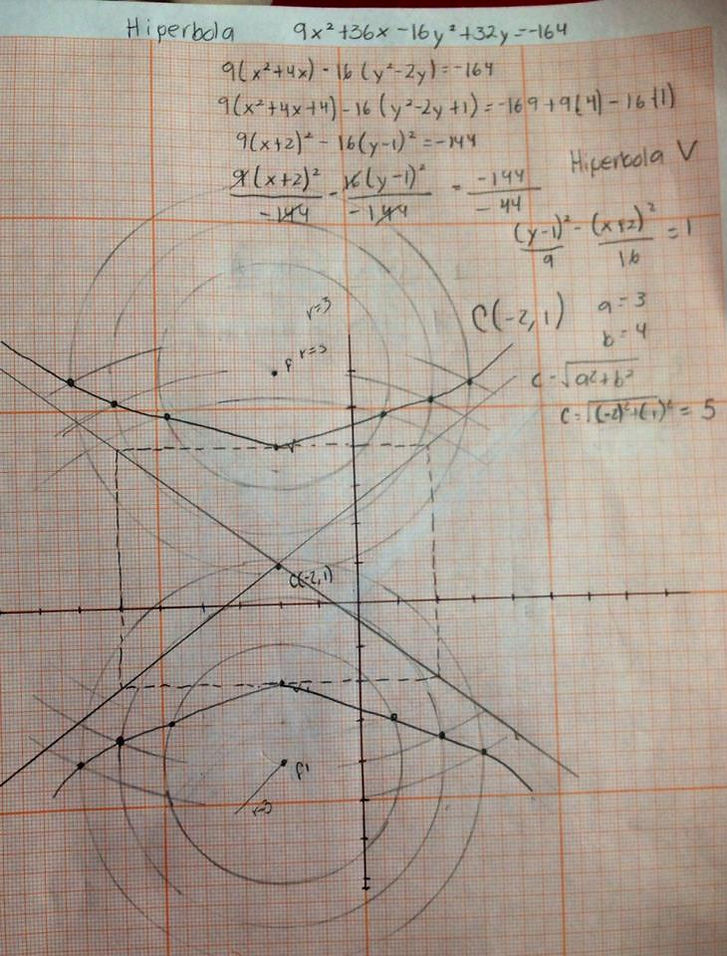
Ejercicio:
En este video pude identificar las secciones cónicas por medio del discriminante.
Reflexión: En este tema mis dificultades se basaron en identificar si era una circunferencia, parábola, elipse o una hipérbola sin embargo con las clases y la práctica ahora me resulta mucho más sencillo
bottom of page